Getting Started with Stereo Vision

With our current resources, we have started with using a pair of GoPro Hero 5 sessions for our bench testing needs. By using them to capture still images of calibration targets.

Proposed stereo vision pipeline

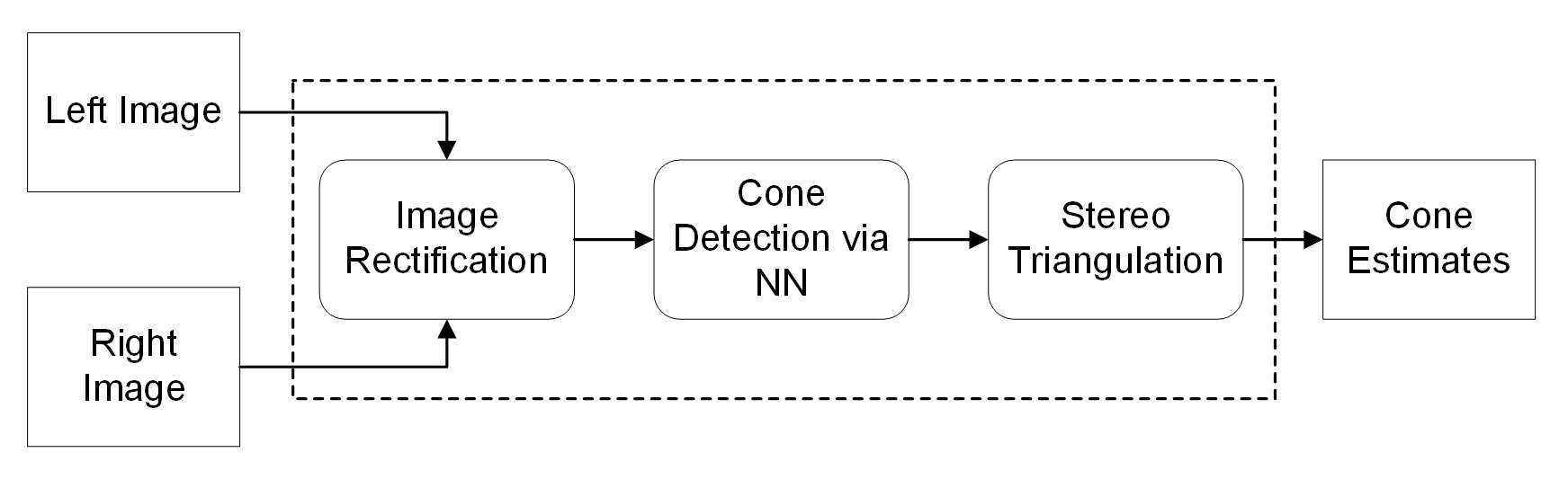
As seen in our proposed stereo vision pipeline above, we plan to follow quite a standard stereo vision pipeline for 3D reconstruction/pose estimation. However, for our use case of cone localisation and detection, certain assumptions and simplifications can be made.

This post will mainly cover our progress on image rectification and stereo triangulation.

Image rectification

Before anything can be done before hand, the raw images have to be processed through a series of rectifications and calibration steps.

\[s\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1\\ r_{21} & r_{22} & r_{23} & t_2\\ r_{31} & r_{32} & r_{33} & t_3\\ \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z\\ 1 \end{bmatrix}\]

First up, is the calibration and undistortion step. In which the intrinsic and extrinsic parameters are found. In which real-world coordinates $(X, Y, Z)$ is projected into the pixel coordinates $(u, v)$.

As epipolar geometry uses some assumptions based on a pin hole camera model, the raw images from most modern-day cameras would still require some distortion correction due to defects within the camera lenses, which occur in both the radial and tangetial directions.

As seen above the GoPros we were using for testing, uses a fish-eyed lense often seen in sports/action point of view cameras as they are often marketed as more “immersive”. However, for our use case such fish-eyed effect is considered a negative and thus was removed by calibration. As seen with a test image above.

So far all that has been done was on a per camera basis, the next step stereo rectification is based on the general stereo setup in which the image planes of the two cameras within the stereo setup are not on the same plane. Rectification conducted to simplify calculations down the pipeline as when the image plane of two cameras coincides, epipolar geometry simplifies down to simple geometry problem of similar triangles. We however, can further simplify things by having the two cameras be mounted on the same plane from the start, which allows us to skip this step.

Stereo Triangulation

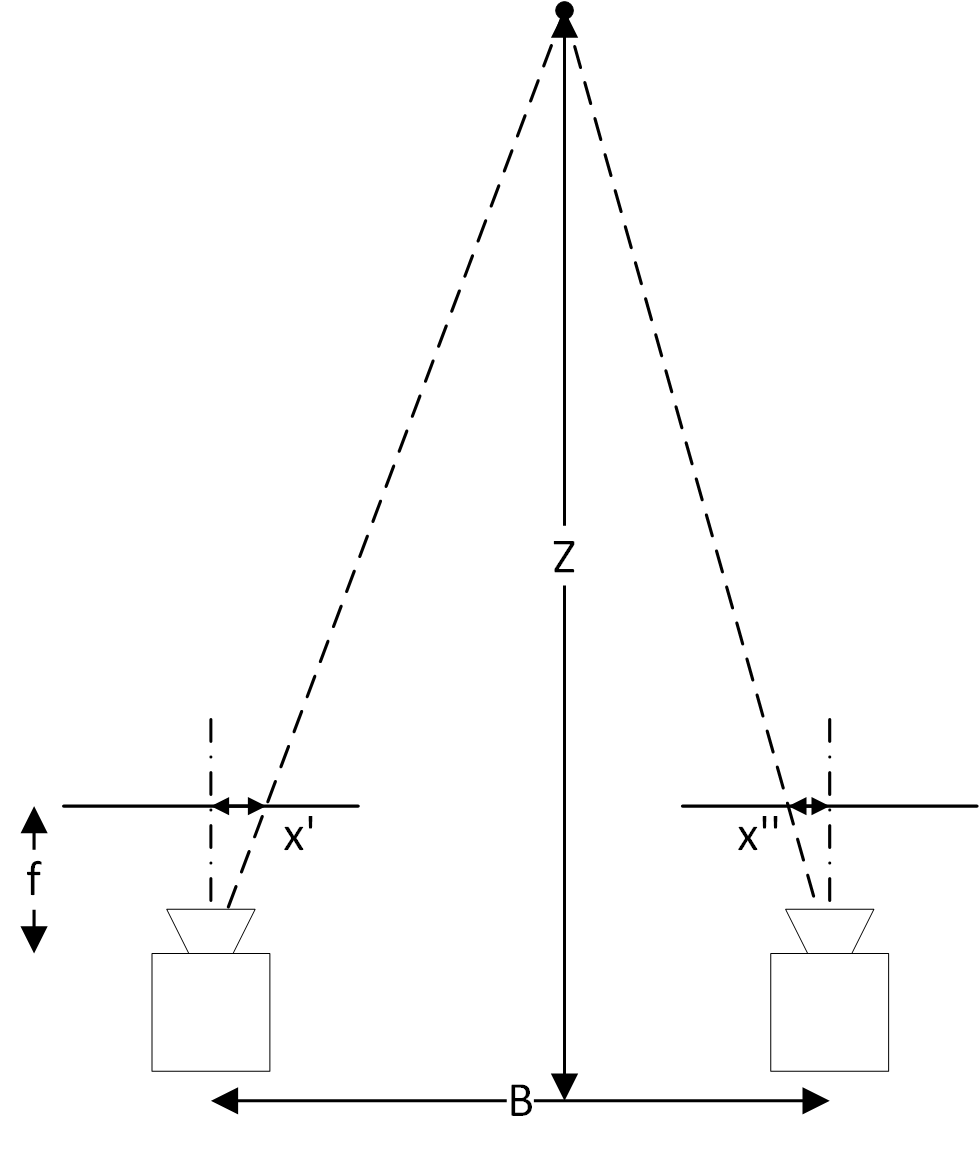
A starting point of stereo triangulation is a simple depth from disparity calculation. As mentioned earlier, epipolar geometry simplifies a problem of similar triangles, as seen in the diagram above. Where, $Z$ is real world depth of the target object, $B$ is the real world baseline (distance between the two camera centers), $f$ is the focal length of the cameras in pixel units, and $x’$ and $x’’$ are pixel location of the target object projected in the left and right image. Thus it is simple to see that depth is simply inversely related to the disparty of the object ($d = x’ - x’’$) or the difference in horizontal pixel coordinates in the left and right image,

\[Z = \dfrac{fB}{d}\]

This is the fundamental calculation used in disparity mapping a related concept to stereo vision, in which a depth map is produced from a pair of stereo image. For our use case however, we are not interested in the depth map of the environment but rather only the cones for tract boundary detection. As seen from the image pipeline from the start cone position will be fed into from an detector neural net, and thus would significantly cut down the require processing compared to a disparity map.