Point Cloud Cylindrical Volume Reconstruction

In this blog post, I would like to go over some of the steps taken to perform cylindrical volume reconstruction. For a bit of context, this particular processing step comes in after we have finished the ground plane segmentation and clustering for the point clouds. However, during the segmentation step, we might have inadvertently remove points which belong to our object of interest, which in this case, are traffic cones.

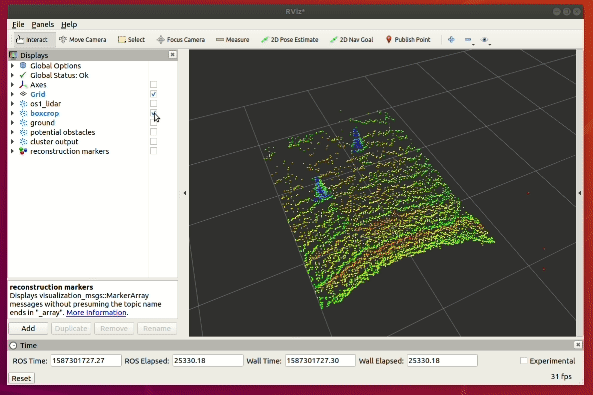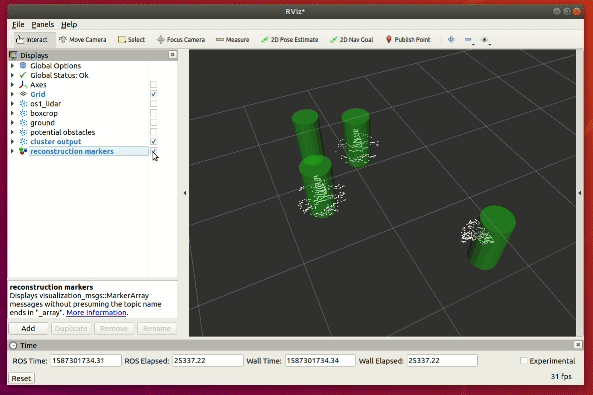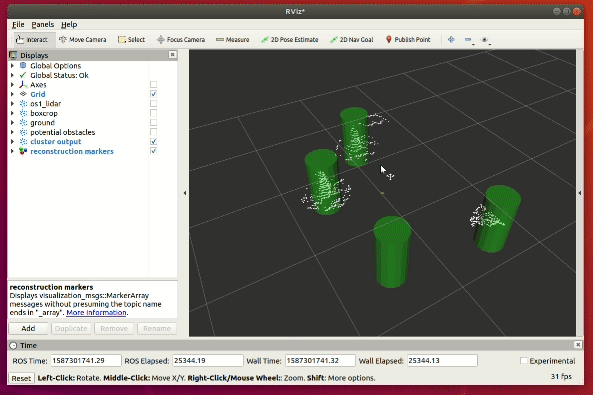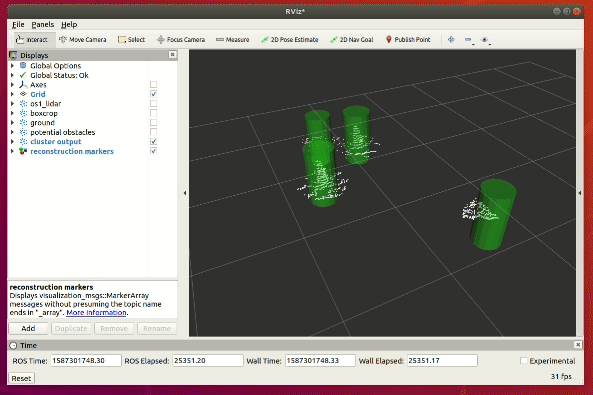
To counteract this potential loss of point cloud data, we apply a cylindrical filter to recover all the neighbouring points for each cluster. The implementation results is shown on the top right gif animation.

This particular process was performed with the help from Point Cloud Library (PCL). However, the documentation regarding this process is somewhat minimal. While there has been some discussion regarding using the pcl::TfQuadraticXYZComparison function to filter out a cylindrical volume here. The details were often incomplete and difficult to comprehend.

The first step is to revisit the source located on github here. From the brief provided, we can see that the filter is provided in a general matrix form for Quadric Surface (not to be confused with Quadratic). It is also stated that the equation used is as follows, where $\star$ is the operator and can be assigned with any of the following $(\lt, \gt, \le, \ge, =)$, and is LT, GT, LE, GE, EQ correspondingly in code.

\[p' A p + 2v' p + c \star 0\]

In this case, we would like to recover the points within the cylinder, so we will use the less-than operator.

\[p' A p + 2v' p + c \lt 0\]

$p$ and $v$ are 3-element vectors, $A$ is a 3-by-3 matrix and $c$ is a scalar. We will see how we can use this to filter out an arbitrary cylinder object.

\[p = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \qquad A = \begin{bmatrix} A & B & C \\ D & E & F \\ G & H & I \\ \end{bmatrix} \qquad v = \begin{bmatrix} J \\ K \\ L \end{bmatrix}\]

Recall that a cylinder with its axis along $z$ has the following general form, where $(a, b)$ represents the centre coordinate of the cylinder on the xy-plane.

\[(x-a)^2 + (y-b)^2 = r^2\]

If we expand and re-arrange general equation of the cylinder, we get the following.

\[x^2 + y^2 - 2ax - 2by + a^2 + b^2 - r^2 = 0\]

The next step is then to match the coefficient so that we have the same cylinder equation but in matrix form. For matrix $A$, all elements would be $0$ except $A=1$ and $E=1$. For vector $v$, we would need $J = -2a$ and $K = -2b$. For the last remaining scalar, we would require the scalar $c = a^2 + b^2 - r^2$. To summarise, we will end up with the following.

\[A = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \qquad v = \begin{bmatrix} -2a \\ -2b \\ 0 \end{bmatrix} \qquad c = a^2 + b^2 - r^2\]

A short C++ code snippet which corresponds to the above description is provided below. Note that this approach does not only apply to this relatively simple cylinder case, but can also be applied to any other Quadric surfaces.

// extract centroid of cluster
pcl::PointXYZ centre;
pcl::computeCentroid(*cloud_cluster, centre);

// set marker properties
set_marker_properties(&marker_array_msg.markers[n], centre, n);

// cylindrical reconstruction from ground points
pcl::ConditionAnd<pcl::PointXYZ>::Ptr cyl_cond (new pcl::ConditionAnd<pcl::PointXYZ> ());

// setup our matrix A
Eigen::Matrix3f cylinderMatrix;
cylinderMatrix(0,0) = 1.0;
cylinderMatrix(1,1) = 1.0;

// setup our vector V
Eigen::Vector3f cylinderV;
cylinderV << -centre.x, -centre.y, 0;

// setup our scalar c
double radius = params.reconst_radius;
float cylinderScalar = - (radius * radius) + centre.x * centre.x + centre.y * centre.y;

pcl::TfQuadraticXYZComparison<pcl::PointXYZ>::Ptr cyl_comp 
    (new pcl::TfQuadraticXYZComparison<pcl::PointXYZ> 
    (pcl::ComparisonOps::LE, cylinderMatrix, cylinderV, cylinderScalar));
cyl_cond->addComparison(cyl_comp);

pcl::PointCloud<pcl::PointXYZ> recovered;

// build and apply filter
condrem.setCondition(cyl_cond);
condrem.setInputCloud(input_ground);
condrem.setKeepOrganized(false);
condrem.filter(recovered);

From a top down view below, we can see that the cylindrical filter works well in recovering the nearby points for each detected cluster.

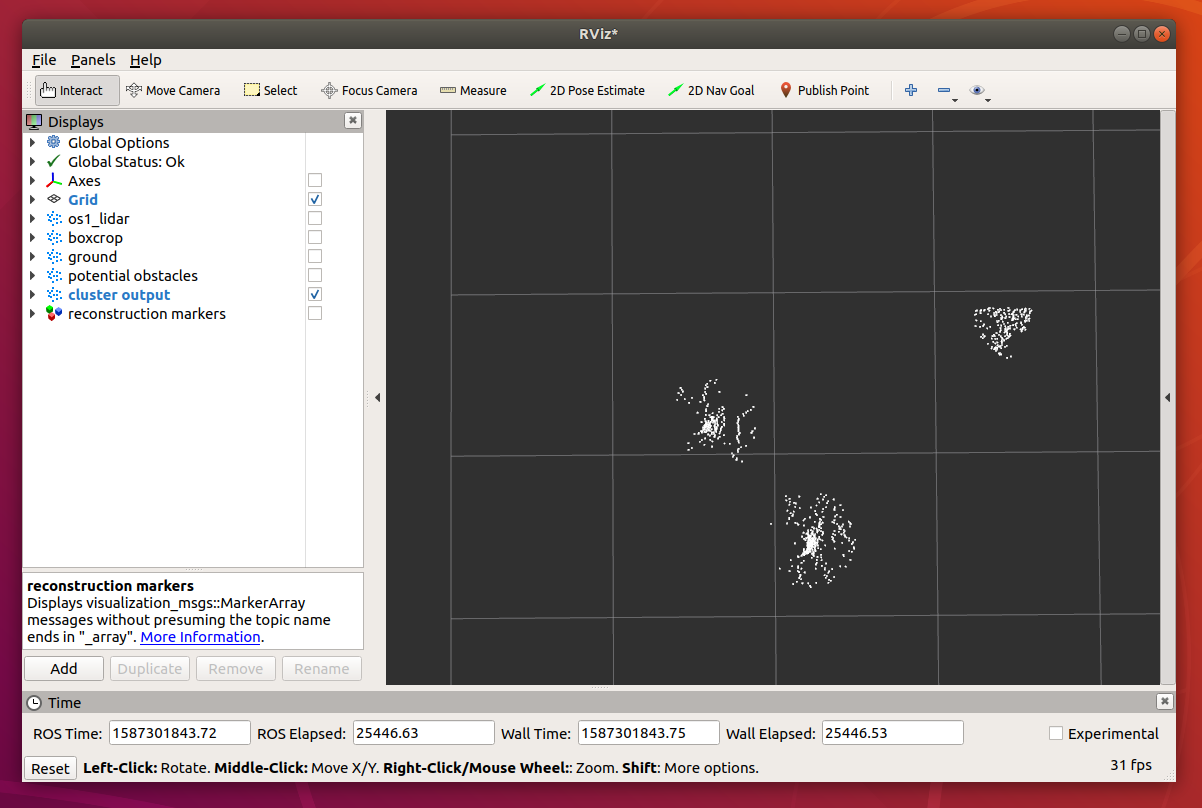
The next step would be to implement a rule-based filter to eliminate clusters with insufficient points, and return the remaining cluster as confirmed traffic cones. Furthermore, the codes would need to be re-factored and optimised to meet our immediate performance requirement.